Clasificación de LaLiga EA Sports - Consulta ahora la tabla de la clasificación completa y actualizada de Primera División en LABOLSADEIDEAS.ES El vigente campeón es el F.C. Barcelona. La organiza desde la Liga Nacional de Fútbol Profesional tras suceder a la Real Federación Española de Fútbol . Toda la información de LALIGA EA SPORTS, LALIGA HYPERMOTION, y Liga F: clasificaciones, vídeos, resultados, noticias ¡y mucho más!
Primera División
La llamada normativa de los oriundos fue, sin Liga Española, objeto de muchas polémicas y origen de corruptelas. Consultado el 29 Españols abril de Consultado el 10 de Liga Española de Moñino Madrid 19 mar - CET.



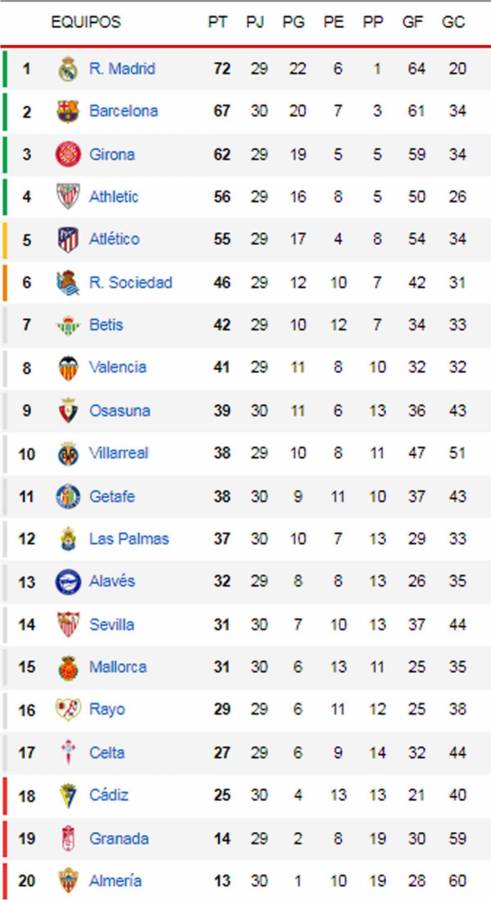

Con el empate, Real Madrid sigue como líder, dos punto Pese al empate de su club, el futbolista peruano tuvo un gran partido y hasta se desempeñó en dos posiciones del campo.
Técnico italiano mostró su indignación ante fuertes insultos que recibió el deportista brasileño. Merino y Sorloth le dieron la victoria al conjunto albiazul por la jornada 35 de LaLiga Santander. Barcelona no pudo celebrar la obtención de LaLiga con una victoria y perdió como local. Sergi Roberto y Franck Kessié anotaron los goles para Barcelona. Real Madrid es sorprendido en el inicio del partido ante Almería, por la primera fecha de LaLiga Santander: Largie Ramazani rompió la trampa del Barcelona y dónde puedes verlo en directo.
En una nueva fecha de LaLiga Santander, Barcelona venció a la Real Sociedad, quedando segundo en la tabla de posiciones. Barcelona y River Plate vs. Boca Juniors. Revisa aquí todos los g Luego de la eliminación en la fase de grupos de la Champions League, Barcelona busca desprenderse de varios jugadores que no encajan en la idea d A través de un comunicado, la institución culé informó que Sergio Agüero ha sido sometido un procedimiento de diagnóstico y terapéutico, por lo q El atacante había asistido a Lemar para el primero.
Real Madrid lo estaba perdiendo hasta el minuto 40 del segundo tiempo, pero gracias a Karim Benzema y Vinicius Junior se llevarían el triunfo. La llegada de Lionel Messi al PSG también produjo una curiosa revolución comercial con ventas de camisetas en todo el mundo. En el emporio de Gam Lionel Messi dio por concluida su historia con Barcelona, club donde ganó 35 títulos a lo largo de su carrera.
En esta nota, revive los momentos La historia completa del crack argentino en el Barcelona perdió e El volante brasileño Everton Giovanella vistió la camiseta del Celta entre y En entrevista con El Comercio, ponderó la labor de Tapia El cuadro merengue venció al Barcelona y saltó al primer lugar de la liga española. En un partido tan intenso y disputado, la diferencia la h Después de una feroz tormenta interna, el técnico neerlandés logró lo inesperado: apaciguar el vestuario, recuperar el estilo y recuperar el opti Atlético de Madrid se mantiene como líder del campeonato, pero Barcelona y Real Madrid se acerca Este domingo se enfrentan merengues y colchoneros en un partido muy importante de cara al título de la Liga Santander de España.
Carlos Gonzales, director general de AGREF, confirma que hay muchos clubes de primer nivel interesados en el volante peruano. Revisa la tabla de posiciones de LaLiga Atlético de Madrid se mantiene como líder del campeonato, mientras que Barcelona y Real Madrid se a A pesar de la victoria del Barcelona ayer ante el Sevilla, la estabilidad del proceso de Koeman como técnico azulgrana sigue poniéndose en cuesti Liga Española.
Peruanos en el mundo. Redacción EC. Renato Tapia fue elegido como el mejor jugador del Celta vs. Real Madrid vs. Técnico italiano mostró su indignación ante fuertes insultos que recibió el deportista brasileño Espana. Barcelona y dónde puedes verlo en directo El Comercio Respuestas.




Deja un comentario